In this article, I’ll review the following 8 classical sorting algorithms, and implement them in Go:

  • bubble sort
  • selection sort
  • insertion sort
  • shell sort
  • merge sort
  • quick sort
  • heap sort
  • radix sort

These basic sorting algorithms are sometimes favored by interviewers, and the ideas of these classical sorting algorithms(like merge sort, quick sort, heap sort, etc.) are sometimes the key points of algorithm problems, so it’s worth taking time on it.

Highly inefficient sorts

Bubble sort

Bubble sort is simple but highly inefficient, so it’s rarely used in practice, unless in situation where inputs data is very small or nearly sorted.

The algorithms is to compare adjsent two numbers, swap them if first is larger than second, from beginning to end. Every time the biggest so far will pop to the right, and every time it takes O(n) time complexity and it needs n times, so the time complexity is O(n2).

bubble sort

1
2
3
4
5
6
7
8
9

func bubbleSort(nums []int) {
	for i, size := 0, len(nums); i < size; i++ {
		for j := 0; j < size-i-1; j++ {
			if nums[j] > nums[j+1] {
				nums[j], nums[j+1] = nums[j+1], nums[j]
			}
		}
	}
}

Simple sorts

Two of the simplest sorts are insertion sort and selection sort, both of which are efficient on small data.

Selection sort

Selection sort is very simple:

  1. find the minimum in the list
  2. swap with the i index

Its time complexity is O(n2).

selection sort

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

func selectionSort(nums []int) {
	for i := 0; i < len(nums)-1; i++ {
		minIndex := i
		for j := i + 1; j < len(nums); j++ {
			if nums[j] < nums[minIndex] {
				minIndex = j
			}
		}
		nums[i], nums[minIndex] = nums[minIndex], nums[i]
	}
}

Insertion sort

Insertion sort is used in cases where the input data is small or partly sorted. The idea is to pick one from unsorted list and insert into sorted part.

Its time complexity is O(n2).

insertion sort

1
2
3
4
5
6
7

func insertSort(nums []int) {
	for i := 1; i < len(nums); i++ {
		for j := i; j > 0 && nums[j] < nums[j-1]; j-- {
			nums[j], nums[j-1] = nums[j-1], nums[j]
		}
	}
}

Shell sort

Shell sort improves upon insertion sort by moving out of order elements more than one position at a time. It will separate data by gap and sort each group by insertion sort, and continously decrease gap until it reaches 1, in that case it becomes insertion sort completely.

shell sort

1
2
3
4
5
6
7
8
9

func insertShellSort(nums []int) {
	for gap := len(nums) / 2; gap > 0; gap /= 2 {
		for i := gap; i < len(nums); i++ {
			for j := i; j >= gap && nums[j] < nums[j-gap]; j -= gap {
				nums[j], nums[j-gap] = nums[j-gap], nums[j]
			}
		}
	}
}

Efficient sorts

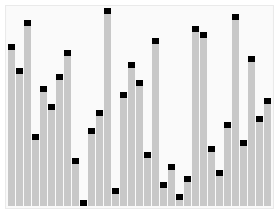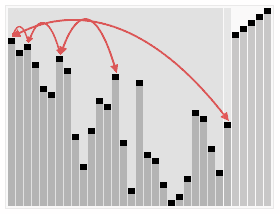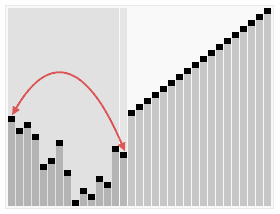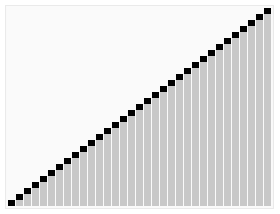
Heap sort

Heapsort is a much more efficient version of selection sort. It also works by determining the largest (or smallest) element of the list, placing that at the end (or beginning) of the list, then continuing with the rest of the list, but accomplishes this task efficiently by using a data structure called a heap, a special type of binary tree.

Using the heap, finding the next largest element takes O(log n) time, instead of O(n) for a linear scan as in simple selection sort. This allows Heapsort to run in O(n log n) time, and this is also the worst case complexity.

heap sort

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

func heapSort(nums []int) {
	heapify(nums)
	for i := len(nums) - 1; i > 0; i-- {
		nums[i], nums[0] = nums[0], nums[i]
		siftDown(nums, 0, i)
	}
}

// modify nums to max heap
func heapify(nums []int) {
	for i := len(nums) / 2; i >= 0; i-- {
		siftDown(nums, i, len(nums))
	}
}

func siftDown(heap []int, lo, hi int) {
	root := lo
	for {
		child := 2*root + 1
		if child >= hi {
			return
		}
		if child+1 < hi && heap[child+1] > heap[child] {
			child++
		}
		if heap[child] > heap[root] {
			heap[child], heap[root] = heap[root], heap[child]
			root = child
		} else {
			return
		}
	}
}

Merge sort

The concept of merge sort: Divide and Conquer is widely used for solving other questions. Basically it works as follows:

  1. If the length of list is smaller or equal than 1, it’s sorted
  2. Divide the list to two sublist and sort them recursively
  3. Merge two sorted list into one

Its time complexity is O(n2), and it needs O(n) space.

merge sort

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

func mergeSort(nums []int) {
	if len(nums) <= 1 {
		return
	}
	middle := len(nums) / 2
	mergeSort(nums[:middle])
	mergeSort(nums[middle:])
	merge(nums, middle)
}

func merge(nums []int, middle int) {
	tmp := make([]int, len(nums))
	i, j, k := 0, middle, 0
	for i < middle && j < len(nums) {
		if nums[i] < nums[j] {
			tmp[k] = nums[i]
			i++
		} else {
			tmp[k] = nums[j]
			j++
		}
		k++
	}

	for i < middle {
		tmp[k] = nums[i]
		k, i = k+1, i+1
	}

	for j < len(nums) {
		tmp[k] = nums[j]
		k, j = k+1, j+1
	}

	for i, v := range tmp {
		nums[i] = v
	}
}

Quick sort

Quicksort is a divide and conquer algorithm which relies on a partition operation: to partition an array, an element called a pivot is selected. All elements smaller than the pivot are moved before it and all greater elements are moved after it. This can be done efficiently in linear time and in-place. The lesser and greater sublists are then recursively sorted. This yields average time complexity of O(n log n), with low overhead, and thus this is a popular algorithm.

quick sort

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

func quickSort(nums []int) {
	if len(nums) == 0 {
		return
	}
	i, j, pivot := 0, len(nums)-1, nums[0]
	for i < j {
		for i < j && nums[j] >= pivot {
			j--
		}
		if i < j {
			nums[i], i = nums[j], i+1
		}
		for i < j && nums[i] < pivot {
			i++
		}
		if i < j {
			nums[j], j = nums[i], j-1
		}
	}
	nums[i] = pivot
	quickSort(nums[:i])
	quickSort(nums[i+1:])
}

Non-comparison sorts

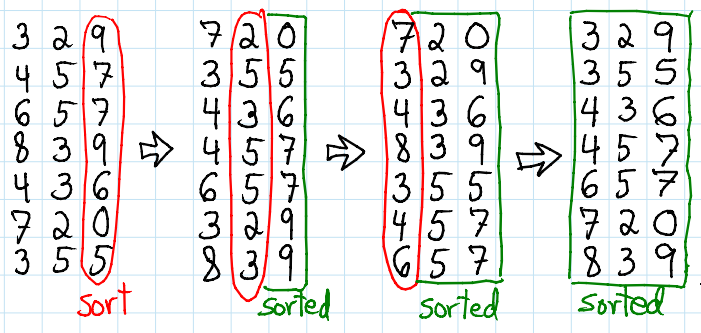
LSD Radix sort

Radix sort is an integer sorting algorithm that sorts data with integer keys by grouping the keys by individual digits that share the same significant position and value (place value).

Radix sort uses counting sort as a subroutine to sort an array of numbers.

radix sort

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51

func radixSort(nums []int) {
    // bucket stores nums in new place, count stores count number of every digit
	bucket, count := make([]int, len(nums)), make([]int, 10)

    // start from the least significant digit(lsd)
	for d := 1; d <= maxBitLen(nums); d++ {
		// zeros the count
		for i := range count {
			count[i] = 0
		}
		// count numbers of every digit
		for _, n := range nums {
			count[digit(n, d)]++
		}
		for i := 1; i < 10; i++ {
			count[i] += count[i-1]
		}
		for i := len(nums) - 1; i >= 0; i-- {
			k := digit(nums[i], d)
			count[k]--
			bucket[count[k]] = nums[i]
		}
		for i, v := range bucket {
			nums[i] = v
		}
	}
}

// Find the max digit length among all numbers in nums
func maxBitLen(nums []int) int {
	var max int
	for _, v := range nums {
		if v > max {
			max = v
		}
	}
	var ret int
	for max > 0 {
		ret, max = ret+1, max/10
	}
	return ret
}

// Find digit of number n at index d
func digit(n, d int) int {
	pow := 1
	for d > 1 {
		pow, d = pow*10, d-1
	}
	return n / pow % 10
}

References